Javakurs/Übungsaufgaben/DiffusionLimitedAggregation: Unterschied zwischen den Versionen
(→Einleitung) |
|||
| Zeile 13: | Zeile 13: | ||
Die Radien der Kreise sollten mit der Größe des DLA-Fraktals wachsen. Dazu überprüft man bei jeder Anlagerung eines Partikels, ob sich das Fraktal vergrößert hat und ändert gegebenenfalls den Radius. Ein Partikel hat außer seiner Existenz keine weiteren besonderen Eigenschaften. | Die Radien der Kreise sollten mit der Größe des DLA-Fraktals wachsen. Dazu überprüft man bei jeder Anlagerung eines Partikels, ob sich das Fraktal vergrößert hat und ändert gegebenenfalls den Radius. Ein Partikel hat außer seiner Existenz keine weiteren besonderen Eigenschaften. | ||
| − | === | + | === Vorüberlegungen === |
Soweit so gut. '''Nun bist du ein wenig gefragt!'''<br/> | Soweit so gut. '''Nun bist du ein wenig gefragt!'''<br/> | ||
Lies dir die folgenden Fragestellungen durch, und denke darüber nach. | Lies dir die folgenden Fragestellungen durch, und denke darüber nach. | ||
| Zeile 38: | Zeile 38: | ||
. | . | ||
| − | === | + | === Lösungen === |
| − | # Ein 2-dimensionales Array von genau der | + | # Ein 2-dimensionales Array von genau der Größe der zu simulierenden Fläche bietet sich an. Als Datentyp würde ''boolean'' genügen, denn wir wollen nur wissen, ob sich an der Position (x,y) ein Partikel befindet oder nicht. Dem Autor ist aber ''int'' sympathischer ;)<br/>''int[][] field = new int[256][256];'' |
| − | # Jedes der 8 benachbarten Felder um die Position des gerade betrachteten Partikels muss | + | # Jedes der 8 benachbarten Felder um die Position des gerade betrachteten Partikels muss überprüft werden. Ist dort ein Partikel vorhanden, so enthält das Feld einen Wert >0. |
| − | # [http://javadocs.org/Math Math.random()] erzeugt | + | # [http://javadocs.org/Math Math.random()] erzeugt zufällige Zahlen. Mit deren Hilfe kann man über eine Fallunterscheidung die X- und Y-Koordinate des Partikels inkrementieren oder dekrementieren. Dadurch bewegt sich das Teilchen einen Schritt weiter. |
== Die Praxis == | == Die Praxis == | ||
| − | Da diese Aufgabe ziemlich komplex ist, werden schrittweise alle | + | Da diese Aufgabe ziemlich komplex ist, werden schrittweise alle nötigen Bausteine entwickelt. |
=== Grafik === | === Grafik === | ||
| − | Zur Grafikdarstellung gibt es die einfach zu bedienende Klasse "Pad", die ein Fenster erstellt in dem du mit einfachen Routinen zeichnen kannst. | + | Zur Grafikdarstellung gibt es die einfach zu bedienende Klasse "Pad", die ein Fenster erstellt, in dem du mit einfachen Routinen zeichnen kannst. |
| − | Falls du noch nicht die | + | Falls du noch nicht die ÜBB-Klassen in deinem Javakurs-Verzeichnis hast, lade dir von [http://uebb.cs.tu-berlin.de/books/java/ der ÜBB-Seite] die Klassen Pad, Point und Terminal herunter und lege sie in das Verzeichnis ab, in dem auch dein Programm entstehen soll. Wenn du dies getan hast, steht dir die Grafikfunktionalität zur Verfügung. In dieser Aufgabe werden die notwendigen Grafikbefehle vorgeben, du musst dir keine Sorgen machen, dass du dies nicht schaffst. |
=== Schritt fuer Schritt === | === Schritt fuer Schritt === | ||
# Erstelle eine Klasse ''DLA'' | # Erstelle eine Klasse ''DLA'' | ||
| − | # | + | # Füge in der ersten Zeile folgenden import hinzu: ''import java.awt.Color;''. Was genau dies bedeutet, wird in [[Javakurs2007/Vortrag06|Vortrag 6]] erklärt. |
| − | # Schreibe eine Methode ''public static int limit(int value, int lower, int upper)'', die | + | # Schreibe eine Methode ''public static int limit(int value, int lower, int upper)'', die überprüft, ob sich der Wert ''value'' innerhalb der Grenzen ''lower'' und ''upper'' befindet. Ist dies nicht der Fall, soll der Wert auf diesen Bereich beschränkt zurückgegeben werden. |
| − | # Schreibe eine Methode ''public static boolean testPixel(int[][]field, int x, int y)'' die | + | # Schreibe eine Methode ''public static boolean testPixel(int[][]field, int x, int y)'', die überprüft, ob an einem bestimmten Punkt im 2-dimensionalen Array ein Wert >0 vorliegt. Fange dabei ungültige Werte für x und y ab. Benutze dazu die ''limit'' Methode. |
| − | # Teste die ''testPixel(...)'' Methode! | + | # Teste die ''testPixel(...)''-Methode! |
| − | # Schreibe eine Methode ''public static boolean isTouching(int[][] field, int x, int y)'' die | + | # Schreibe eine Methode ''public static boolean isTouching(int[][] field, int x, int y)'', die überprüft, ob sich in einem der 8 umliegenden Felder ein Partikel befindet. Benutzte dabei die ''testPixel(...)'' Methode. |
# Teste diese Methode! | # Teste diese Methode! | ||
| − | # Schreibe eine Methode ''public static boolean inRange(int x, int y, int maxR, int maxX, int maxY)'' die | + | # Schreibe eine Methode ''public static boolean inRange(int x, int y, int maxR, int maxX, int maxY)'', die überprüft, ob sich die Koordination ''x'' und ''y'' in einem Rechteck der Seitenlänge ''maxX'' und ''maxY'' innerhalb eines Abstandes ''maxR'' vom Mittelpunkt befindet. |
# Teste diese Methode! | # Teste diese Methode! | ||
| − | # Schreibe eine Methode ''public static int moveRandom(int movePixel)'' die | + | # Schreibe eine Methode ''public static int moveRandom(int movePixel)'', die eine Zahl (Koordinatenkomponente) mit '''gleichen''' Wahrscheinlichkeiten inkrementiert (+1), unverändert lässt (+/-0) oder erniedrigt (-1). |
# Test kurz diese Methode. | # Test kurz diese Methode. | ||
| − | # Schreibe die Methode ''public static void setPixel(Pad drawPad, int[][]field, int x, int y, Color c)''. Diese | + | # Schreibe die Methode ''public static void setPixel(Pad drawPad, int[][]field, int x, int y, Color c)''. Diese überprüft noch einmal die Gültigkeit der Koordinaten ''x'' und ''y'', platziert dann im Array ''field'' an diesen Koordinaten einen Partikel und zeichnet den Partikel auf dem ''drawPad'' wie folgt: |
drawPad.setColor(c); | drawPad.setColor(c); | ||
drawPad.drawDot(x, y); | drawPad.drawDot(x, y); | ||
=== Main === | === Main === | ||
| − | Schreibe nun die main-Methode | + | Schreibe nun die main-Methode für das DLA-Programm. |
| − | Wenn dir die Struktur des Programms schon klar ist, dann kannst du gern allein | + | Wenn dir die Struktur des Programms schon klar ist, dann kannst du gern allein versuchen, das Problem zu lösen. Hier sei noch ein Code-Fragment zum Berechnen von Koordinaten auf einem Kreis gegeben: |
//einen Punkt auf einem Kreis um den Mittelpunkt mit dem Radius | //einen Punkt auf einem Kreis um den Mittelpunkt mit dem Radius | ||
Version vom 11. April 2007, 11:49 Uhr
Inhaltsverzeichnis
Einleitung
Als Diffusion Limited Aggregation, kurz DLA, bezeichnet man physikalische Vorgaenge bei denen sich Teilchen durch Brownsche Bewegung zufällig bewegen und bei Kontakt mit anderen Teilchen anlagern. Diese Vorgänge können leicht am Computer simuliert werden und erzeugen sehr schöne Gebilde. In dieser Aufgabe soll es darum gehen, eine solche DLA-Simulation zu programmieren.
Eine solches Programm könnte z.B. so aussehen:
Die Theorie
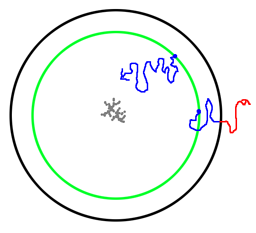
Um ein möglichst gleichmäßiges Wachstum des DLA-Fraktals zu erreichen, setzt man in der Mitte des Bildschirms einen Keim und lässt auf einer Kreisbahn (grün) um das Zentrum einen neuen Partikel erscheinen. Diesen Partikel bewegt man zufällig über die Ebene (blaue Bahnen). Entfernt sich der Partikel zu weit vom Zentrum (schwarzer Kreis), so wird er verworfen (rote Bahn) und ein neuer Partikel erzeugt.
Die Radien der Kreise sollten mit der Größe des DLA-Fraktals wachsen. Dazu überprüft man bei jeder Anlagerung eines Partikels, ob sich das Fraktal vergrößert hat und ändert gegebenenfalls den Radius. Ein Partikel hat außer seiner Existenz keine weiteren besonderen Eigenschaften.
Vorüberlegungen
Soweit so gut. Nun bist du ein wenig gefragt!
Lies dir die folgenden Fragestellungen durch, und denke darüber nach.
- Die Partikel werden in einer 2-dimensionalen Ebene gespeichert. Welche Datenstruktur aus Java kann man besonders gut verwenden, um viele Partikel abzuspeichern?
- Wie würde man überprüfen, ob ein Partikel einen anderen berührt?
- Wie kann man einen Partikel über die Fläche bewegen? Wie erzeugt man eine Brownsche Bewegung?
.
.
.
.
.
.
.
.
Lösungen
- Ein 2-dimensionales Array von genau der Größe der zu simulierenden Fläche bietet sich an. Als Datentyp würde boolean genügen, denn wir wollen nur wissen, ob sich an der Position (x,y) ein Partikel befindet oder nicht. Dem Autor ist aber int sympathischer ;)
int[][] field = new int[256][256]; - Jedes der 8 benachbarten Felder um die Position des gerade betrachteten Partikels muss überprüft werden. Ist dort ein Partikel vorhanden, so enthält das Feld einen Wert >0.
- Math.random() erzeugt zufällige Zahlen. Mit deren Hilfe kann man über eine Fallunterscheidung die X- und Y-Koordinate des Partikels inkrementieren oder dekrementieren. Dadurch bewegt sich das Teilchen einen Schritt weiter.
Die Praxis
Da diese Aufgabe ziemlich komplex ist, werden schrittweise alle nötigen Bausteine entwickelt.
Grafik
Zur Grafikdarstellung gibt es die einfach zu bedienende Klasse "Pad", die ein Fenster erstellt, in dem du mit einfachen Routinen zeichnen kannst.
Falls du noch nicht die ÜBB-Klassen in deinem Javakurs-Verzeichnis hast, lade dir von der ÜBB-Seite die Klassen Pad, Point und Terminal herunter und lege sie in das Verzeichnis ab, in dem auch dein Programm entstehen soll. Wenn du dies getan hast, steht dir die Grafikfunktionalität zur Verfügung. In dieser Aufgabe werden die notwendigen Grafikbefehle vorgeben, du musst dir keine Sorgen machen, dass du dies nicht schaffst.
Schritt fuer Schritt
- Erstelle eine Klasse DLA
- Füge in der ersten Zeile folgenden import hinzu: import java.awt.Color;. Was genau dies bedeutet, wird in Vortrag 6 erklärt.
- Schreibe eine Methode public static int limit(int value, int lower, int upper), die überprüft, ob sich der Wert value innerhalb der Grenzen lower und upper befindet. Ist dies nicht der Fall, soll der Wert auf diesen Bereich beschränkt zurückgegeben werden.
- Schreibe eine Methode public static boolean testPixel(int[][]field, int x, int y), die überprüft, ob an einem bestimmten Punkt im 2-dimensionalen Array ein Wert >0 vorliegt. Fange dabei ungültige Werte für x und y ab. Benutze dazu die limit Methode.
- Teste die testPixel(...)-Methode!
- Schreibe eine Methode public static boolean isTouching(int[][] field, int x, int y), die überprüft, ob sich in einem der 8 umliegenden Felder ein Partikel befindet. Benutzte dabei die testPixel(...) Methode.
- Teste diese Methode!
- Schreibe eine Methode public static boolean inRange(int x, int y, int maxR, int maxX, int maxY), die überprüft, ob sich die Koordination x und y in einem Rechteck der Seitenlänge maxX und maxY innerhalb eines Abstandes maxR vom Mittelpunkt befindet.
- Teste diese Methode!
- Schreibe eine Methode public static int moveRandom(int movePixel), die eine Zahl (Koordinatenkomponente) mit gleichen Wahrscheinlichkeiten inkrementiert (+1), unverändert lässt (+/-0) oder erniedrigt (-1).
- Test kurz diese Methode.
- Schreibe die Methode public static void setPixel(Pad drawPad, int[][]field, int x, int y, Color c). Diese überprüft noch einmal die Gültigkeit der Koordinaten x und y, platziert dann im Array field an diesen Koordinaten einen Partikel und zeichnet den Partikel auf dem drawPad wie folgt:
drawPad.setColor(c); drawPad.drawDot(x, y);
Main
Schreibe nun die main-Methode für das DLA-Programm. Wenn dir die Struktur des Programms schon klar ist, dann kannst du gern allein versuchen, das Problem zu lösen. Hier sei noch ein Code-Fragment zum Berechnen von Koordinaten auf einem Kreis gegeben:
//einen Punkt auf einem Kreis um den Mittelpunkt mit dem Radius //maxR+20 erzeugen double x = Math.toRadians(Math.random()*360); int movingPixelX = limit((int)(Math.cos(x)*(maxR+20))+maxX/2, 0, maxX); int movingPixelY = limit((int)(Math.sin(x)*(maxR+20))+maxY/2, 0, maxY);
Falls dir noch nicht ganz klar ist, wie alles zusammen wirken soll, benutze folgenden Rumpf, der schon die Grafik-Funktionalitaet und andere Vorgaben enthaellt:
import java.awt.Color;
class DLA {
public static void main(String[] args) {
//Feld fuer Kollisionsueberpruefung erstellen
int[][] field = ...
//Grenzen fuer Koordinaten der Partikel aus field berechnen (.length verwenden)
int maxX = ...
int maxY = ...
//Fenster fuer Grafikausgabe vorbereiten und anzeigen
Pad drawPad = new Pad();
drawPad.setBackground(Pad.black);
drawPad.setPadSize(maxX, maxY);
drawPad.setVisible(true);
drawPad.setColor(Pad.white);
//"Samen" erzeugen. Also den ersten Partikel in der Mitte des Feldes setzen
setPixel(...);
//Radius des Partikels der am weitesten vom Zentrum entfernt ist
int maxR=0;
//Schleifenkopf, solange maxR nicht den Rand des Fensters
//beruehrt, sollen neue Punkte gezeichnet werden
while(...) {
//einen Punkt auf einem Kreis um den Mittelpunkt mit dem Radius
//maxR+20 erzeugen
double x = Math.toRadians(Math.random()*360);
int movingPixelX = limit((int)(Math.cos(x)*(maxR+20))+maxX/2, 0, maxX);
int movingPixelY = limit((int)(Math.sin(x)*(maxR+20))+maxY/2, 0, maxY);
//Schleife zum bewegen des Partikels
//while(!isTouching(...)) && inRange(..., ..., maxR+30, ..., ...))
{
//Partikelkoordinaten zufaellig bewegen (moveRandom)
movingPixelX = ...
movingPixelY = ...
}
//Schleife zuende, ueberpruefe ob eine Beruehrung vorliegt:
if(isTouching(...)) {
//Farbwertberechnung fuer 1337 blau-Effekt
int k = limit(255-(int)(255*((double)maxR*2)/(double)maxX), 0, 255);
Color c = new Color(k, k, 255);
//den Partikel setzen und zeichnen
setPixel(...);
//Radius zum Mittelpunkt berechnen,
//wenn groesser als altes Maximum, ueberschreiben
...
}
}
return;
}
...
}
Hinweis: Koordinaten im Computer
Am Computer werden Koordination, historisch bedingt, anders behandelt als im rechtwinkligen Koordinatensystem. Koordination im Computer werden von links nach rechts, als X-Achse und von oben nach unten als Y-Achse berechnet. Beachte dies bei der Verwendung von drawPad.drawDot(x,y).
(0,0)-------------------- X | (640,0) | | | | | | (0,480) (640,480) Y
Kommentare
Wenn du Anmerkungen zur Aufgabe hast oder Lob und Kritik loswerden möchtest ist hier die richtige Stelle dafür. Klicke einfach ganz rechts auf "bearbeiten" und schreibe deinen Kommentar direkt ins Wiki. Keine Scheu, es geht nichts kaputt ;)