Javakurs/Übungsaufgaben/DiffusionLimitedAggregation: Unterschied zwischen den Versionen
K (→Schritt fuer Schritt) |
(→Schritt fuer Schritt) |
||
| (11 dazwischenliegende Versionen von 8 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Einleitung == | == Einleitung == | ||
| − | Als [http://en.wikipedia.org/wiki/Diffusion-limited_aggregation Diffusion Limited Aggregation], kurz DLA, bezeichnet man physikalische | + | Als [http://en.wikipedia.org/wiki/Diffusion-limited_aggregation Diffusion Limited Aggregation], kurz DLA, bezeichnet man physikalische Vorgänge, bei denen sich Teilchen durch [[wikipedia:Brownsche Bewegung| Brownsche Bewegung]] zufällig bewegen und bei Kontakt mit anderen Teilchen an diese anlagern. Diese Vorgänge können leicht am Computer simuliert werden und erzeugen sehr schöne Gebilde, die zu der Klasse der [http://de.wikipedia.org/wiki/Fraktal Fraktale] gehören. In dieser Aufgabe soll es darum gehen, eine solche DLA-Simulation zu programmieren. |
Eine solches Programm könnte z.B. so aussehen: | Eine solches Programm könnte z.B. so aussehen: | ||
| Zeile 9: | Zeile 9: | ||
== Die Theorie == | == Die Theorie == | ||
| − | + | ||
| + | Zu Beginn der DLA ist das Feld leer. Zuerst wird ein Pixel in die Mitte des Feldes gesetzt, an dieser Stelle befindet sich der erste Partikel.<br/> | ||
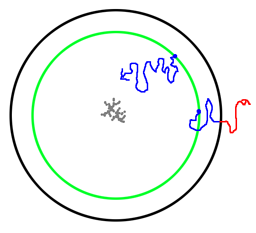
| + | Nun wird auf einer gedachten Kreisbahn (grün) um das Zentrum ein weiterer Partikel erzeugt, der sich an einer zufälligen Position auf dieser Kreisbahn befindet. Von diesem Startpunkt aus bewegt sich der Partikel nun zufällig nach oben, unten, links oder rechts (z.B. auf einer der blauen Bahnen). Er bewegt sich solange, bis er entweder zu weit weg vom Zentrum ist (den schwarzen Kreis verlässt), oder bis er auf einen bereits vorhandenen Partikel stößt. In diesem Fall lagert er sich dort an, das heißt, er bleibt fest an dieser Position und dort kann ein Pixel gezeichnet werden. Sollte der Partikel hingegen den schwarzen Kreis verlassen haben, wird er verworfen (rote Bahn) und es wird stattdessen wieder ein neuer Partikel auf der grünen Kreisbahn erzeugt. Auch nach Anlagern eines Partikels wird wieder ein neuer erzeugt und der Vorgang wiederholt sich. | ||
[[Bild:Dla_mechanism.png]] | [[Bild:Dla_mechanism.png]] | ||
| − | + | Ein Partikel hat außer seiner Existenz keine weiteren besonderen Eigenschaften. Ist er einmal fest, bewegt er sich nicht mehr. Es werden solange Partikel erzeugt, bewegt und gegebenenfalls angelagert, bis einer der Partikel das Feld verlässt. Geschieht dies, so ist die DLA beendet und die Zeichnung fertig.<br/> | |
| + | Wurde ein Partikel angelagert, so wird der maximale Radius (= Abstand des äußersten Partikels vom Zentrum) aktualisiert, falls der neue Partikel weiter vom Zentrum entfernt ist als alle anderen. Dieser Abstand ist wichtig, da sich aus ihm die grüne und die schwarze Kreisbahn berechnen. Das heißt, je mehr Partikel sich anlagern, desto größer werden die Radien der Kreise. Das heißt auch, die Zeichnung ist erst fertig, wenn der schwarze Kreis an die Grenze des Feldes stößt, da sich erst dann ein Partikel aus dem Feld heraus bewegen kann. | ||
| + | |||
| + | Das Gebilde, das durch die Anlagerung der Partikel entstanden ist, nennt man Fraktal. | ||
=== Vorüberlegungen === | === Vorüberlegungen === | ||
| Zeile 19: | Zeile 24: | ||
Lies dir die folgenden Fragestellungen durch, und denke darüber nach. | Lies dir die folgenden Fragestellungen durch, und denke darüber nach. | ||
| − | # Die Partikel werden in einer 2-dimensionalen Ebene gespeichert. Welche Datenstruktur aus Java kann man besonders gut verwenden, um | + | # Die Partikel werden in einer 2-dimensionalen Ebene gespeichert. Welche Datenstruktur aus Java kann man besonders gut verwenden, um für jeden Punkt einer Ebene zu speichern, ob sich dort ein Partikel befindet? |
| − | # Wie würde man überprüfen, ob | + | # Wie würde man überprüfen, ob der sich gerade bewegende Partikel einen anderen berührt? |
# Wie kann man einen Partikel über die Fläche bewegen? Wie erzeugt man eine [http://en.wikipedia.org/wiki/Brownian_motion Brownsche Bewegung]? | # Wie kann man einen Partikel über die Fläche bewegen? Wie erzeugt man eine [http://en.wikipedia.org/wiki/Brownian_motion Brownsche Bewegung]? | ||
| Zeile 41: | Zeile 46: | ||
=== Lösungen === | === Lösungen === | ||
| − | # Ein 2-dimensionales Array von genau der Größe | + | # Ein 2-dimensionales Array von genau der Größe des Feldes bietet sich an. Die erste Dimension entspricht der x-Koordinaten, die zweite der y-Koordinaten. Somit kann für jede Position (x,y) gespeichert werden, ob sich dort ein Partikel befindet oder nicht. Als Datentyp würde ''boolean'' genügen, dem Autor ist aber ''int'' sympathischer ;) Befindet sich an der Position ein Partikel, ist der Wert des Arrays an der Stelle größer als 0, befindet sich dort keiner, ist der Wert 0.<br/>''int[][] field = new int[256][256];'' Beachte: Anders als beim Koordinatensystem, das du aus Mathe kennst, ist hier (0,0) der Punkt ganz oben links und es wird nach rechts und nach unten hochgezählt. (Siehe unten) |
| − | # Jedes der 8 benachbarten Felder um die Position des gerade betrachteten Partikels muss überprüft werden. Ist dort ein Partikel vorhanden, so enthält das Feld einen Wert >0. | + | # Jedes der 8 benachbarten Felder um die Position (x,y) des gerade betrachteten Partikels muss überprüft werden. Ist dort ein Partikel vorhanden, so enthält das Feld einen Wert >0 an einer der Positionen. |
| − | # [http://javadocs.org/Math Math.random()] erzeugt zufällige Zahlen. Mit deren Hilfe kann man über eine Fallunterscheidung die X- und Y-Koordinate des Partikels inkrementieren oder dekrementieren. Dadurch bewegt sich das Teilchen einen Schritt weiter. | + | # [http://javadocs.org/Math Math.random()] erzeugt zufällige Zahlen. Mit deren Hilfe kann man über eine Fallunterscheidung die X- und Y-Koordinate des Partikels inkrementieren oder dekrementieren, d.h. um 1 erhöhen oder um 1 verringern. Dadurch bewegt sich das Teilchen einen Schritt weiter. |
== Die Praxis == | == Die Praxis == | ||
| Zeile 50: | Zeile 55: | ||
Zur Grafikdarstellung gibt es die einfach zu bedienende Klasse "Pad", die ein Fenster erstellt, in dem du mit einfachen Routinen zeichnen kannst. | Zur Grafikdarstellung gibt es die einfach zu bedienende Klasse "Pad", die ein Fenster erstellt, in dem du mit einfachen Routinen zeichnen kannst. | ||
| − | Falls du noch nicht die ÜBB-Klassen in deinem Javakurs-Verzeichnis hast, lade dir von [http://uebb | + | Falls du noch nicht die ÜBB-Klassen in deinem Javakurs-Verzeichnis hast, lade dir von [http://www.uebb.tu-berlin.de/menue/forschung/buecher/pepper_programmieren_lernen_eine_grundlegende_einfuehrung_mit_java_1_und_2_auflage/ der ÜBB-Seite] die Klassen Pad, Point und Terminal herunter und lege sie in das Verzeichnis ab, in dem auch dein Programm entstehen soll. Wenn du dies getan hast, steht dir die Grafikfunktionalität zur Verfügung. In dieser Aufgabe werden die notwendigen Grafikbefehle vorgeben, du musst dir keine Sorgen machen, dass du dies nicht schaffst. |
=== Schritt fuer Schritt === | === Schritt fuer Schritt === | ||
# Erstelle eine Klasse ''DLA'' | # Erstelle eine Klasse ''DLA'' | ||
| − | # Füge in der ersten Zeile folgenden import hinzu: ''import java.awt.Color;''. Was genau dies bedeutet, wird in | + | # Füge in der ersten Zeile folgenden import hinzu: ''import java.awt.Color;''. Was genau dies bedeutet, wird in Vortrag 6 erklärt. |
| − | # Schreibe eine Methode ''public static int limit(int value, int lower, int upper)'', die überprüft, ob sich der Wert ''value'' innerhalb der Grenzen ''lower'' und ''upper'' befindet. Ist dies nicht der Fall, soll der Wert auf diesen Bereich beschränkt zurückgegeben werden. | + | # Schreibe eine Methode ''public static int limit(int value, int lower, int upper)'', die überprüft, ob sich der Wert ''value'' innerhalb der Grenzen ''lower'' und ''upper'' befindet. Ist dies nicht der Fall, soll der Wert auf diesen Bereich beschränkt zurückgegeben werden, d.h. falls der Eingabewert zu groß war, wird er auf "upper" gesetzt; war zu klein, wird er auf "lower" gesetzt. |
# Schreibe eine Methode ''public static boolean testPixel(int[][]field, int x, int y)'', die überprüft, ob an einem bestimmten Punkt im 2-dimensionalen Array ein Wert >0 vorliegt. Fange dabei ungültige Werte für x und y ab. Benutze dazu die ''limit'' Methode. | # Schreibe eine Methode ''public static boolean testPixel(int[][]field, int x, int y)'', die überprüft, ob an einem bestimmten Punkt im 2-dimensionalen Array ein Wert >0 vorliegt. Fange dabei ungültige Werte für x und y ab. Benutze dazu die ''limit'' Methode. | ||
# Teste die ''testPixel(...)''-Methode! | # Teste die ''testPixel(...)''-Methode! | ||
| Zeile 62: | Zeile 67: | ||
# Schreibe eine Methode ''public static boolean inRange(int x, int y, int maxR, int maxX, int maxY)'', die überprüft, ob sich die Koordination ''x'' und ''y'' in einem Rechteck der Seitenlänge ''maxX'' und ''maxY'' innerhalb eines Abstandes ''maxR'' vom Mittelpunkt befindet. | # Schreibe eine Methode ''public static boolean inRange(int x, int y, int maxR, int maxX, int maxY)'', die überprüft, ob sich die Koordination ''x'' und ''y'' in einem Rechteck der Seitenlänge ''maxX'' und ''maxY'' innerhalb eines Abstandes ''maxR'' vom Mittelpunkt befindet. | ||
# Teste diese Methode! | # Teste diese Methode! | ||
| − | # Schreibe eine Methode ''public static int moveRandom(int movePixel)'', die eine Zahl (Koordinatenkomponente) mit '''gleichen''' Wahrscheinlichkeiten inkrementiert (+1), unverändert lässt (+/-0) oder | + | # Schreibe eine Methode ''public static int moveRandom(int movePixel)'', die eine Zahl (Koordinatenkomponente) mit '''gleichen''' Wahrscheinlichkeiten inkrementiert (+1), unverändert lässt (+/-0) oder verringert (-1). |
# Test kurz diese Methode. | # Test kurz diese Methode. | ||
| − | # Schreibe die Methode ''public static void setPixel(Pad drawPad, int[][]field, int x, int y, | + | # Schreibe die Methode ''public static void setPixel(Pad drawPad, int[][]field, int x, int y, Color c)''. Diese überprüft noch einmal, ob die Koordinaten ''x'' und ''y'' im erlaubten Bereich des field liegen, platziert dann im Array ''field'' an diesen Koordinaten einen Partikel und zeichnet den Partikel auf dem ''drawPad'' wie folgt: |
| + | |||
drawPad.setColor(c); | drawPad.setColor(c); | ||
drawPad.drawDot(x, y); | drawPad.drawDot(x, y); | ||
| + | |||
| + | Die Klasse Color wird in der Java Dokumentation natürlich erklärt: http://java.sun.com/j2se/1.5.0/docs/api/java/awt/Color.html | ||
| + | Du kannst mit ''Color.black'' auf vordefinierte Farbe zugreifen oder neue Farben über ihre RGB Werte erstellen. | ||
=== Main === | === Main === | ||
Schreibe nun die main-Methode für das DLA-Programm. | Schreibe nun die main-Methode für das DLA-Programm. | ||
| − | Wenn dir die Struktur des Programms schon klar ist, dann kannst du gern allein versuchen, das Problem zu lösen. | + | Wenn dir die Struktur des Programms schon klar ist, dann kannst du gern allein versuchen, das Problem zu lösen. |
| − | // | + | Hier sei als Hilfestellung noch ein Code-Fragment gegeben, das die Koordinaten eines zufälligen Punktes auf der Kreisbahn berechnet, die dem grünen Kreis im obigen Theoriebeispiel entspricht. Der Mittelpunkt dieses Kreises ist der Mittelpunkt des Feldes und der Radius ist maxR + 20. |
| − | // | + | |
| + | // auf einem gedachten Kreis um den Mittelpunkt mit Radius maxR + 20 einen Partikel "erzeugen" | ||
| + | // d.h. die Koordinaten eines zufaelligen Punktes auf dem Kreisrand berechnen | ||
| + | // neuer Partikel ist somit an Position movingPixelX ; movingPixelY | ||
| + | |||
double x = Math.toRadians(Math.random()*360); | double x = Math.toRadians(Math.random()*360); | ||
int movingPixelX = limit((int)(Math.cos(x)*(maxR+20))+maxX/2, 0, maxX); | int movingPixelX = limit((int)(Math.cos(x)*(maxR+20))+maxX/2, 0, maxX); | ||
| Zeile 81: | Zeile 94: | ||
//Fenster fuer Grafikausgabe vorbereiten und anzeigen | //Fenster fuer Grafikausgabe vorbereiten und anzeigen | ||
| + | |||
Pad drawPad = new Pad(); | Pad drawPad = new Pad(); | ||
drawPad.setBackground(Pad.black); | drawPad.setBackground(Pad.black); | ||
| Zeile 99: | Zeile 113: | ||
class DLA { | class DLA { | ||
public static void main(String[] args) { | public static void main(String[] args) { | ||
| − | //Feld | + | //Feld erstellen, in dem gespeichert wird, ob an gegebenen Koordinaten ein Partikel ist |
int[][] field = ... | int[][] field = ... | ||
| − | |||
| − | // | + | //Maximalwerte fuer Koordinaten der Partikel, lassen sich aus den Dimensionen von field berechnen (.length verwenden) |
int maxX = ... | int maxX = ... | ||
int maxY = ... | int maxY = ... | ||
| − | + | ||
//Fenster fuer Grafikausgabe vorbereiten und anzeigen | //Fenster fuer Grafikausgabe vorbereiten und anzeigen | ||
Pad drawPad = new Pad(); | Pad drawPad = new Pad(); | ||
| Zeile 114: | Zeile 127: | ||
drawPad.setColor(Pad.white); | drawPad.setColor(Pad.white); | ||
| − | + | //"Samen" erzeugen, also den ersten Pixel aufs Feld setzen (Color: Pad.white) | |
| − | //"Samen" erzeugen | + | // Hier: Pixel wird genau in die Mitte des Feldes gesetzt - andere Startpixel waeren moeglich |
setPixel(...); | setPixel(...); | ||
| − | // | + | //Abstand des Partikels, der am weitesten vom Zentrum des Feldes entfernt ist |
int maxR=0; | int maxR=0; | ||
| − | // | + | //Abbruchbedingung: Hat einer der Partikel sich aus dem Feld heraus bewegt? |
| − | // | + | boolean isAtBorder = false; |
| + | |||
| + | //Schleife: Erstelle solange neue Partikel, wie die Abbruchbedingung false ist | ||
while(...) { | while(...) { | ||
| − | // | + | // auf einem gedachten Kreis um den Mittelpunkt mit Radius maxR + 20 einen Partikel "erzeugen" |
| − | + | // d.h. die Koordinaten eines zufaelligen Punktes auf dem Kreisrand berechnen | |
| + | // neuer Partikel ist somit an Position movingPixelX ; movingPixelY | ||
double x = Math.toRadians(Math.random()*360); | double x = Math.toRadians(Math.random()*360); | ||
int movingPixelX = limit((int)(Math.cos(x)*(maxR+20))+maxX/2, 0, maxX); | int movingPixelX = limit((int)(Math.cos(x)*(maxR+20))+maxX/2, 0, maxX); | ||
int movingPixelY = limit((int)(Math.sin(x)*(maxR+20))+maxY/2, 0, maxY); | int movingPixelY = limit((int)(Math.sin(x)*(maxR+20))+maxY/2, 0, maxY); | ||
| − | // | + | // Nun Start der brownschen Bewegung |
| − | + | // Partikel bewegt sich, bis er einen bereits vorhandenen Partikel beruehrt oder bis er das Feld verlaesst | |
| + | while(!isTouching(...) && inRange(..., ..., maxR+30, ..., ...)) | ||
{ | { | ||
//Partikelkoordinaten zufaellig bewegen (moveRandom) | //Partikelkoordinaten zufaellig bewegen (moveRandom) | ||
| Zeile 138: | Zeile 155: | ||
} | } | ||
| − | // | + | // Brownsche Bewegung zu Ende - Ist Partikel auf einen bereits vorhandenen Partikel gestossen? |
if(isTouching(...)) { | if(isTouching(...)) { | ||
| − | + | // Wenn ja: Partikel ist jetzt "fest" an dieser Stelle, zeichne einen Punkt dort | |
| − | + | // Farbwertberechnung fuer 1337 blau-Effekt | |
| − | + | int k = limit(255-(int)(255*((double)maxR*2)/(double)maxX), 0, 255); | |
| − | + | Color c = new Color(k, k, 255); | |
| − | + | ||
| − | + | //den Partikel setzen und zeichnen | |
| − | + | setPixel(...); | |
| − | + | ||
| − | + | // Abstand des neu gesetzten Partikels zum Mittelpunkt des Feldes berechnen | |
| − | + | // wenn groesser als alter maximaler Abstand maxR, dann Maximum mit neuem Abstandswert ueberschreiben | |
| + | |||
| + | maxR = (int) Math.max(..., ...); | ||
| + | |||
| + | // Falls der Partikel das Feld verlassen hat: Zeichnung ist fertig, setze Abbruchkriterium der aeusseren Schleife auf true | ||
| + | if (...) { | ||
| + | isAtBorder = true; | ||
| + | } | ||
} | } | ||
} | } | ||
| Zeile 181: | Zeile 205: | ||
<!-- | <!-- | ||
Als kleine Starthilfe folgt ein Beispiel, wie so ein Kommentar formatiert sein könnte. Mit "Vorschau zeigen" kannst du dir ansehen, was deine Änderung bewirken würde, ohne wirklich etwas zu ändern. | Als kleine Starthilfe folgt ein Beispiel, wie so ein Kommentar formatiert sein könnte. Mit "Vorschau zeigen" kannst du dir ansehen, was deine Änderung bewirken würde, ohne wirklich etwas zu ändern. | ||
| − | Du musst übrigens außerhalb dieses auskommentieren Bereichs schreiben ;) | + | Du musst übrigens außerhalb dieses auskommentieren Bereichs schreiben ;) --> |
| − | ==== Robert | + | === Georg === |
| + | Super Aufgabe :) Macht Spaß die Bilder zu erstellen ;) | ||
| + | |||
| + | Braucht bei mir aber leider relativ lange, wäre interessant wie man die Simulation maximal beschleunigt. Interessant ist weiterhin das das Bildaufbauen bei mir zu Hause signifikant länger braucht als @TUB. | ||
| + | |||
| + | === Robert === | ||
Na mal schauen, ob irgendjemand diese Funktion wirklich benutzt. Ich fände es jedenfalls toll. | Na mal schauen, ob irgendjemand diese Funktion wirklich benutzt. Ich fände es jedenfalls toll. | ||
| − | - | + | |
| + | === Dirks Verbesserungsvorschläge === | ||
| + | |||
| + | testPixel in isPixel oder isPixelEmpty | ||
| + | movePixel in movingPixelKoordinate umbenennen | ||
| + | |||
| + | moveRandome in moveKoordinateRandome | ||
| + | |||
| + | === Brandons Kommentar === | ||
| + | Die Anweisung für setPixel ist Irreführend. Bei der jetzigen Formulierung geht man davon aus das das Einfügen von "drawPad.setColor(c); | ||
| + | drawPad.drawDot(x, y);" ausreicht. Dabei muss man das Einfügen des Punktes in das Array selber erstellen. (z.B: field[x][y] = 1) | ||
| + | Besser wäre vielleicht: Diese überprüft noch einmal die Gültigkeit der Koordinaten x und y, platziert dann im Array field an diesen Koordinaten einen Partikel und dann wird der Partikel auf dem drawPad wie folgt gezeichnet: oder so. | ||
| + | |||
| + | === Theresa === | ||
| + | Ich habe mal die theoretische Beschreibung des Algorithmus etwas ausgebaut und die Vorgabe der main-Methode etwas umfangreicher gestaltet. | ||
| + | |||
| + | [[Kategorie:Java]] | ||
| + | [[Kategorie:Java_Aufgaben]] | ||
| + | |||
| + | __NOTOC__ | ||
Aktuelle Version vom 5. März 2014, 16:03 Uhr
Einleitung
Als Diffusion Limited Aggregation, kurz DLA, bezeichnet man physikalische Vorgänge, bei denen sich Teilchen durch Brownsche Bewegung zufällig bewegen und bei Kontakt mit anderen Teilchen an diese anlagern. Diese Vorgänge können leicht am Computer simuliert werden und erzeugen sehr schöne Gebilde, die zu der Klasse der Fraktale gehören. In dieser Aufgabe soll es darum gehen, eine solche DLA-Simulation zu programmieren.
Eine solches Programm könnte z.B. so aussehen:
Lass dich jetzt nicht von der scheinbaren Komplexität des Programms abschrecken! Es ist nicht komplex UND du wirst schrittweise zur Lösung geführt. Am Ende kannst du dann noch ein wenig selbst mit dem Programm experimentieren.
Die Theorie
Zu Beginn der DLA ist das Feld leer. Zuerst wird ein Pixel in die Mitte des Feldes gesetzt, an dieser Stelle befindet sich der erste Partikel.
Nun wird auf einer gedachten Kreisbahn (grün) um das Zentrum ein weiterer Partikel erzeugt, der sich an einer zufälligen Position auf dieser Kreisbahn befindet. Von diesem Startpunkt aus bewegt sich der Partikel nun zufällig nach oben, unten, links oder rechts (z.B. auf einer der blauen Bahnen). Er bewegt sich solange, bis er entweder zu weit weg vom Zentrum ist (den schwarzen Kreis verlässt), oder bis er auf einen bereits vorhandenen Partikel stößt. In diesem Fall lagert er sich dort an, das heißt, er bleibt fest an dieser Position und dort kann ein Pixel gezeichnet werden. Sollte der Partikel hingegen den schwarzen Kreis verlassen haben, wird er verworfen (rote Bahn) und es wird stattdessen wieder ein neuer Partikel auf der grünen Kreisbahn erzeugt. Auch nach Anlagern eines Partikels wird wieder ein neuer erzeugt und der Vorgang wiederholt sich.
Ein Partikel hat außer seiner Existenz keine weiteren besonderen Eigenschaften. Ist er einmal fest, bewegt er sich nicht mehr. Es werden solange Partikel erzeugt, bewegt und gegebenenfalls angelagert, bis einer der Partikel das Feld verlässt. Geschieht dies, so ist die DLA beendet und die Zeichnung fertig.
Wurde ein Partikel angelagert, so wird der maximale Radius (= Abstand des äußersten Partikels vom Zentrum) aktualisiert, falls der neue Partikel weiter vom Zentrum entfernt ist als alle anderen. Dieser Abstand ist wichtig, da sich aus ihm die grüne und die schwarze Kreisbahn berechnen. Das heißt, je mehr Partikel sich anlagern, desto größer werden die Radien der Kreise. Das heißt auch, die Zeichnung ist erst fertig, wenn der schwarze Kreis an die Grenze des Feldes stößt, da sich erst dann ein Partikel aus dem Feld heraus bewegen kann.
Das Gebilde, das durch die Anlagerung der Partikel entstanden ist, nennt man Fraktal.
Vorüberlegungen
Soweit so gut. Nun bist du ein wenig gefragt!
Lies dir die folgenden Fragestellungen durch, und denke darüber nach.
- Die Partikel werden in einer 2-dimensionalen Ebene gespeichert. Welche Datenstruktur aus Java kann man besonders gut verwenden, um für jeden Punkt einer Ebene zu speichern, ob sich dort ein Partikel befindet?
- Wie würde man überprüfen, ob der sich gerade bewegende Partikel einen anderen berührt?
- Wie kann man einen Partikel über die Fläche bewegen? Wie erzeugt man eine Brownsche Bewegung?
.
.
.
.
.
.
.
.
Lösungen
- Ein 2-dimensionales Array von genau der Größe des Feldes bietet sich an. Die erste Dimension entspricht der x-Koordinaten, die zweite der y-Koordinaten. Somit kann für jede Position (x,y) gespeichert werden, ob sich dort ein Partikel befindet oder nicht. Als Datentyp würde boolean genügen, dem Autor ist aber int sympathischer ;) Befindet sich an der Position ein Partikel, ist der Wert des Arrays an der Stelle größer als 0, befindet sich dort keiner, ist der Wert 0.
int[][] field = new int[256][256]; Beachte: Anders als beim Koordinatensystem, das du aus Mathe kennst, ist hier (0,0) der Punkt ganz oben links und es wird nach rechts und nach unten hochgezählt. (Siehe unten) - Jedes der 8 benachbarten Felder um die Position (x,y) des gerade betrachteten Partikels muss überprüft werden. Ist dort ein Partikel vorhanden, so enthält das Feld einen Wert >0 an einer der Positionen.
- Math.random() erzeugt zufällige Zahlen. Mit deren Hilfe kann man über eine Fallunterscheidung die X- und Y-Koordinate des Partikels inkrementieren oder dekrementieren, d.h. um 1 erhöhen oder um 1 verringern. Dadurch bewegt sich das Teilchen einen Schritt weiter.
Die Praxis
Da diese Aufgabe ziemlich komplex ist, werden schrittweise alle nötigen Bausteine entwickelt.
Grafik
Zur Grafikdarstellung gibt es die einfach zu bedienende Klasse "Pad", die ein Fenster erstellt, in dem du mit einfachen Routinen zeichnen kannst.
Falls du noch nicht die ÜBB-Klassen in deinem Javakurs-Verzeichnis hast, lade dir von der ÜBB-Seite die Klassen Pad, Point und Terminal herunter und lege sie in das Verzeichnis ab, in dem auch dein Programm entstehen soll. Wenn du dies getan hast, steht dir die Grafikfunktionalität zur Verfügung. In dieser Aufgabe werden die notwendigen Grafikbefehle vorgeben, du musst dir keine Sorgen machen, dass du dies nicht schaffst.
Schritt fuer Schritt
- Erstelle eine Klasse DLA
- Füge in der ersten Zeile folgenden import hinzu: import java.awt.Color;. Was genau dies bedeutet, wird in Vortrag 6 erklärt.
- Schreibe eine Methode public static int limit(int value, int lower, int upper), die überprüft, ob sich der Wert value innerhalb der Grenzen lower und upper befindet. Ist dies nicht der Fall, soll der Wert auf diesen Bereich beschränkt zurückgegeben werden, d.h. falls der Eingabewert zu groß war, wird er auf "upper" gesetzt; war zu klein, wird er auf "lower" gesetzt.
- Schreibe eine Methode public static boolean testPixel(int[][]field, int x, int y), die überprüft, ob an einem bestimmten Punkt im 2-dimensionalen Array ein Wert >0 vorliegt. Fange dabei ungültige Werte für x und y ab. Benutze dazu die limit Methode.
- Teste die testPixel(...)-Methode!
- Schreibe eine Methode public static boolean isTouching(int[][] field, int x, int y), die überprüft, ob sich in einem der 8 umliegenden Felder ein Partikel befindet. Benutzte dabei die testPixel(...) Methode.
- Teste diese Methode!
- Schreibe eine Methode public static boolean inRange(int x, int y, int maxR, int maxX, int maxY), die überprüft, ob sich die Koordination x und y in einem Rechteck der Seitenlänge maxX und maxY innerhalb eines Abstandes maxR vom Mittelpunkt befindet.
- Teste diese Methode!
- Schreibe eine Methode public static int moveRandom(int movePixel), die eine Zahl (Koordinatenkomponente) mit gleichen Wahrscheinlichkeiten inkrementiert (+1), unverändert lässt (+/-0) oder verringert (-1).
- Test kurz diese Methode.
- Schreibe die Methode public static void setPixel(Pad drawPad, int[][]field, int x, int y, Color c). Diese überprüft noch einmal, ob die Koordinaten x und y im erlaubten Bereich des field liegen, platziert dann im Array field an diesen Koordinaten einen Partikel und zeichnet den Partikel auf dem drawPad wie folgt:
drawPad.setColor(c); drawPad.drawDot(x, y);
Die Klasse Color wird in der Java Dokumentation natürlich erklärt: http://java.sun.com/j2se/1.5.0/docs/api/java/awt/Color.html Du kannst mit Color.black auf vordefinierte Farbe zugreifen oder neue Farben über ihre RGB Werte erstellen.
Main
Schreibe nun die main-Methode für das DLA-Programm. Wenn dir die Struktur des Programms schon klar ist, dann kannst du gern allein versuchen, das Problem zu lösen.
Hier sei als Hilfestellung noch ein Code-Fragment gegeben, das die Koordinaten eines zufälligen Punktes auf der Kreisbahn berechnet, die dem grünen Kreis im obigen Theoriebeispiel entspricht. Der Mittelpunkt dieses Kreises ist der Mittelpunkt des Feldes und der Radius ist maxR + 20.
// auf einem gedachten Kreis um den Mittelpunkt mit Radius maxR + 20 einen Partikel "erzeugen" // d.h. die Koordinaten eines zufaelligen Punktes auf dem Kreisrand berechnen // neuer Partikel ist somit an Position movingPixelX ; movingPixelY double x = Math.toRadians(Math.random()*360); int movingPixelX = limit((int)(Math.cos(x)*(maxR+20))+maxX/2, 0, maxX); int movingPixelY = limit((int)(Math.sin(x)*(maxR+20))+maxY/2, 0, maxY);
zusätzlich noch Code um das Grafikfenster zu initialisieren:
//Fenster fuer Grafikausgabe vorbereiten und anzeigen Pad drawPad = new Pad(); drawPad.setBackground(Pad.black); drawPad.setPadSize(maxX, maxY); drawPad.setVisible(true); drawPad.setColor(Pad.white);
Die Klasse Pad bietet ausserdem einige Farbwerte vom Typ Color an, dir du einfach so benutzen kannst.
Pad.white Pad.black ...
Falls dir noch nicht ganz klar ist, wie alles zusammen wirken soll, benutze folgenden Rumpf, der schon die Grafik-Funktionalität und andere Vorgaben enthält:
import java.awt.Color;
class DLA {
public static void main(String[] args) {
//Feld erstellen, in dem gespeichert wird, ob an gegebenen Koordinaten ein Partikel ist
int[][] field = ...
//Maximalwerte fuer Koordinaten der Partikel, lassen sich aus den Dimensionen von field berechnen (.length verwenden)
int maxX = ...
int maxY = ...
//Fenster fuer Grafikausgabe vorbereiten und anzeigen
Pad drawPad = new Pad();
drawPad.setBackground(Pad.black);
drawPad.setPadSize(maxX, maxY);
drawPad.setVisible(true);
drawPad.setColor(Pad.white);
//"Samen" erzeugen, also den ersten Pixel aufs Feld setzen (Color: Pad.white)
// Hier: Pixel wird genau in die Mitte des Feldes gesetzt - andere Startpixel waeren moeglich
setPixel(...);
//Abstand des Partikels, der am weitesten vom Zentrum des Feldes entfernt ist
int maxR=0;
//Abbruchbedingung: Hat einer der Partikel sich aus dem Feld heraus bewegt?
boolean isAtBorder = false;
//Schleife: Erstelle solange neue Partikel, wie die Abbruchbedingung false ist
while(...) {
// auf einem gedachten Kreis um den Mittelpunkt mit Radius maxR + 20 einen Partikel "erzeugen"
// d.h. die Koordinaten eines zufaelligen Punktes auf dem Kreisrand berechnen
// neuer Partikel ist somit an Position movingPixelX ; movingPixelY
double x = Math.toRadians(Math.random()*360);
int movingPixelX = limit((int)(Math.cos(x)*(maxR+20))+maxX/2, 0, maxX);
int movingPixelY = limit((int)(Math.sin(x)*(maxR+20))+maxY/2, 0, maxY);
// Nun Start der brownschen Bewegung
// Partikel bewegt sich, bis er einen bereits vorhandenen Partikel beruehrt oder bis er das Feld verlaesst
while(!isTouching(...) && inRange(..., ..., maxR+30, ..., ...))
{
//Partikelkoordinaten zufaellig bewegen (moveRandom)
movingPixelX = ...
movingPixelY = ...
}
// Brownsche Bewegung zu Ende - Ist Partikel auf einen bereits vorhandenen Partikel gestossen?
if(isTouching(...)) {
// Wenn ja: Partikel ist jetzt "fest" an dieser Stelle, zeichne einen Punkt dort
// Farbwertberechnung fuer 1337 blau-Effekt
int k = limit(255-(int)(255*((double)maxR*2)/(double)maxX), 0, 255);
Color c = new Color(k, k, 255);
//den Partikel setzen und zeichnen
setPixel(...);
// Abstand des neu gesetzten Partikels zum Mittelpunkt des Feldes berechnen
// wenn groesser als alter maximaler Abstand maxR, dann Maximum mit neuem Abstandswert ueberschreiben
maxR = (int) Math.max(..., ...);
// Falls der Partikel das Feld verlassen hat: Zeichnung ist fertig, setze Abbruchkriterium der aeusseren Schleife auf true
if (...) {
isAtBorder = true;
}
}
}
return;
}
...
}
Hinweis: Koordinaten im Computer
Am Computer werden Koordination, historisch bedingt, anders behandelt als im rechtwinkligen Koordinatensystem. Koordination im Computer werden von links nach rechts, als X-Achse und von oben nach unten als Y-Achse berechnet. Beachte dies bei der Verwendung von drawPad.drawDot(x,y).
(0,0)-------------------- X | (640,0) | | | | | | (0,480) (640,480) Y
Kommentare
Wenn du Anmerkungen zur Aufgabe hast oder Lob und Kritik loswerden möchtest, ist hier die richtige Stelle dafür. Klicke einfach ganz rechts auf "bearbeiten" und schreibe deinen Kommentar direkt ins Wiki. Keine Scheu, es geht nichts kaputt ;)
Georg
Super Aufgabe :) Macht Spaß die Bilder zu erstellen ;)
Braucht bei mir aber leider relativ lange, wäre interessant wie man die Simulation maximal beschleunigt. Interessant ist weiterhin das das Bildaufbauen bei mir zu Hause signifikant länger braucht als @TUB.
Robert
Na mal schauen, ob irgendjemand diese Funktion wirklich benutzt. Ich fände es jedenfalls toll.
Dirks Verbesserungsvorschläge
testPixel in isPixel oder isPixelEmpty movePixel in movingPixelKoordinate umbenennen
moveRandome in moveKoordinateRandome
Brandons Kommentar
Die Anweisung für setPixel ist Irreführend. Bei der jetzigen Formulierung geht man davon aus das das Einfügen von "drawPad.setColor(c); drawPad.drawDot(x, y);" ausreicht. Dabei muss man das Einfügen des Punktes in das Array selber erstellen. (z.B: field[x][y] = 1) Besser wäre vielleicht: Diese überprüft noch einmal die Gültigkeit der Koordinaten x und y, platziert dann im Array field an diesen Koordinaten einen Partikel und dann wird der Partikel auf dem drawPad wie folgt gezeichnet: oder so.
Theresa
Ich habe mal die theoretische Beschreibung des Algorithmus etwas ausgebaut und die Vorgabe der main-Methode etwas umfangreicher gestaltet.