Informatik 3/Gedächtnisprotokoll Klausur SS07: Unterschied zwischen den Versionen
(→Aufgabe 4: Graphen) |
(→1. Aufgabe: Multiple Choice) |
||
| Zeile 2: | Zeile 2: | ||
* .. | * .. | ||
| − | * | + | * Traversierung mit Breitensuche erzeugt einen aufspannenden Baum. |
* Die Höhe eines binären Suchbaumes ist immer um 1 größer, als das Maximum der Höhen seiner Teilbäume. | * Die Höhe eines binären Suchbaumes ist immer um 1 größer, als das Maximum der Höhen seiner Teilbäume. | ||
* Für jedes endliche Optimierungsproblem kann man einen Backtrackingalgorithmus finden der dieses löst. | * Für jedes endliche Optimierungsproblem kann man einen Backtrackingalgorithmus finden der dieses löst. | ||
Version vom 26. Juli 2007, 15:10 Uhr
Inhaltsverzeichnis
1. Aufgabe: Multiple Choice
- ..
- Traversierung mit Breitensuche erzeugt einen aufspannenden Baum.
- Die Höhe eines binären Suchbaumes ist immer um 1 größer, als das Maximum der Höhen seiner Teilbäume.
- Für jedes endliche Optimierungsproblem kann man einen Backtrackingalgorithmus finden der dieses löst.
- Für jedes endliche Optimierungsproblem kann man einen Greedy-algorithmus finden der dieses löst.
HashTables
Hashtabelle der Größe 4.
- Hashfunktion: h(k) = k mod 4
- Kollisonsauflösung"double hashing" a(k) = k+2
Vier Werte mit Schlüsseln einfügen und Kollisionen zählen.
(A,5) (B,11) (C,9) (D,14)
A -> 1
B -> 3
C -> 1, 3, 1 , 3 .. (kann nicht eingefügt werden)
D -> 2
0 blieb leer.
Ist die Anzahl der Kollisionen bei double hashing abhängig von der Reihenfolge in der die Elemente eingefügt werden? Begründung, ggf. Beispiel.
AVL-Bäume
- Einfügen in AVL-Baum
- Einfügen in AVL-Baum
- Löschen aus AVL-Baum
Rot-Schwaz-Bäume
- Einfügen in RS-Baum
- Java-Programm schreiben für Höhenberechnung eines Rot-Schwarz-Baumes getBlackHeight(Node root)
- Rot-Schwarz-Baum als gültig vorausgesetzt.
- Vorgegebene Implementation:
- isRed(Node node);
- isBlack(Node node);
- class Node{ int color; Node left; Node right; }
B-Baum
- Element in B-Baum einfügen.
Aufgabe 4: Graphen
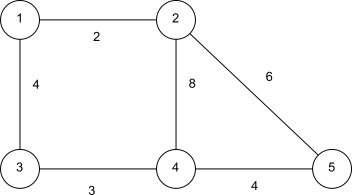
a) Baue eine Adjazenzmatrix zu folgendem Graphen:
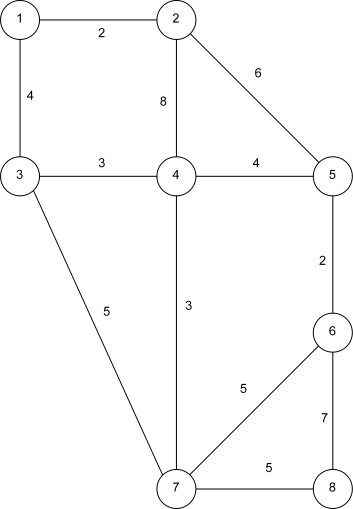
b) Dijkstra auf folgendem Graph ausführen:
c) Definiere (formal oder als Text) den Begriff "aufspannender Baum".
d) Führe union(D,F) auf folgender, als Wald realisierter disjunkter Menge aus: (Graph folgt)
e) Erstelle den Restflussgraphen zu folgendem Flussgraphen: (Graph folgt)
Aufgabe 5: Übungsorganisation
Hab ich, trag ich gleich ein TomyLobo
Aufgabe 6: Dynamisches Programmieren
Hab ich, trag ich gleich ein TomyLobo
Aufgabe 7: Geld wechseln
Hab ich, trag ich gleich ein TomyLobo