Informatik 3/Gedächtnisprotokoll Klausur SS07: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
== Aufgabe 1: Multiple Choice == | == Aufgabe 1: Multiple Choice == | ||
| + | Kreuzen Sie jeweils wahr bzw. falsch an: | ||
* .. | * .. | ||
* Traversierung mit Breitensuche erzeugt einen aufspannenden Baum. | * Traversierung mit Breitensuche erzeugt einen aufspannenden Baum. | ||
| Zeile 25: | Zeile 26: | ||
<br> | <br> | ||
| − | == Aufgabe 3: | + | |
| + | == Aufgabe 3: Suchbäume == | ||
'''AVL-Bäume''' | '''AVL-Bäume''' | ||
*Einfügen in AVL-Baum | *Einfügen in AVL-Baum | ||
| Zeile 32: | Zeile 34: | ||
<br> | <br> | ||
| − | '''Rot/ | + | '''Rot/Schwarz-Bäume''' |
*Einfügen in RS-Baum | *Einfügen in RS-Baum | ||
| − | *Java-Programm schreiben für Höhenberechnung eines Rot-Schwarz-Baumes getBlackHeight(Node root) | + | *Java-Programm schreiben für Höhenberechnung eines Rot-Schwarz-Baumes: int getBlackHeight(Node root) |
** Rot-Schwarz-Baum als gültig vorausgesetzt. | ** Rot-Schwarz-Baum als gültig vorausgesetzt. | ||
** Vorgegebene Implementation: | ** Vorgegebene Implementation: | ||
| − | *** isRed(Node node); | + | *** boolean isRed(Node node); |
| − | *** isBlack(Node node); | + | *** boolean isBlack(Node node); |
*** class Node{ int color; Node left; Node right; } | *** class Node{ int color; Node left; Node right; } | ||
<br> | <br> | ||
| Zeile 44: | Zeile 46: | ||
'''B-Baum''' | '''B-Baum''' | ||
* Element in B-Baum einfügen. | * Element in B-Baum einfügen. | ||
| − | + | <br> | |
== Aufgabe 4: Graphen == | == Aufgabe 4: Graphen == | ||
| Zeile 94: | Zeile 96: | ||
== Aufgabe 6: Dynamisches Programmieren == | == Aufgabe 6: Dynamisches Programmieren == | ||
| + | [[Bild:Info3-ss2007-6.png]] | ||
| + | <!-- Das Bild wurde gerendert mit freundlicher, allerdings unwissender, Unterstützung der deutschen Wikipedia. | ||
| + | Hier der TeX-Quellcode des obenstehenden Bildes: | ||
<math>g(m, n) = \left\lbrace\begin{matrix} 42 & m = 0 \or n=0 \\ g(m-1, n-1) + g(m, n-1) & m > 0 \and n > 0 \end{matrix}\right.</math> | <math>g(m, n) = \left\lbrace\begin{matrix} 42 & m = 0 \or n=0 \\ g(m-1, n-1) + g(m, n-1) & m > 0 \and n > 0 \end{matrix}\right.</math> | ||
| − | + | --> | |
| − | |||
a) Geben Sie eine nicht-rekursive Java-Methode an, die g(m,n) für m, n e N \ {0} berechnet. Die Methode soll dafür polynomielle Laufzeit benötigen | a) Geben Sie eine nicht-rekursive Java-Methode an, die g(m,n) für m, n e N \ {0} berechnet. Die Methode soll dafür polynomielle Laufzeit benötigen | ||
Version vom 26. Juli 2007, 19:16 Uhr
Inhaltsverzeichnis
Aufgabe 1: Multiple Choice
Kreuzen Sie jeweils wahr bzw. falsch an:
- ..
- Traversierung mit Breitensuche erzeugt einen aufspannenden Baum.
- Die Höhe eines binären Suchbaumes ist immer um 1 größer, als das Maximum der Höhen seiner Teilbäume.
- Für jedes endliche Optimierungsproblem kann man einen Backtrackingalgorithmus finden der dieses löst.
- Für jedes endliche Optimierungsproblem kann man einen Greedy-algorithmus finden der dieses löst.
Aufgabe 2: HashTables
Hashtabelle der Größe 4.
- Hashfunktion: h(k) = k mod 4
- Kollisonsauflösung"double hashing" a(k) = k+2
Vier Werte mit Schlüsseln einfügen und Kollisionen zählen.
(A,5) (B,11) (C,9) (D,14)
A -> 1
B -> 3
C -> 1, 3, 1 , 3 .. (kann nicht eingefügt werden)
D -> 2
0 blieb leer.
Ist die Anzahl der Kollisionen bei double hashing abhängig von der Reihenfolge in der die Elemente eingefügt werden? Begründung, ggf. Beispiel.
Aufgabe 3: Suchbäume
AVL-Bäume
- Einfügen in AVL-Baum
- Einfügen in AVL-Baum
- Löschen aus AVL-Baum
Rot/Schwarz-Bäume
- Einfügen in RS-Baum
- Java-Programm schreiben für Höhenberechnung eines Rot-Schwarz-Baumes: int getBlackHeight(Node root)
- Rot-Schwarz-Baum als gültig vorausgesetzt.
- Vorgegebene Implementation:
- boolean isRed(Node node);
- boolean isBlack(Node node);
- class Node{ int color; Node left; Node right; }
B-Baum
- Element in B-Baum einfügen.
Aufgabe 4: Graphen
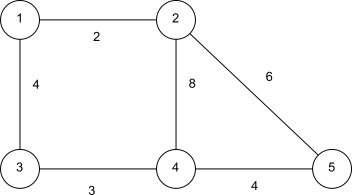
a) Baue eine Adjazenzmatrix zu folgendem Graphen:
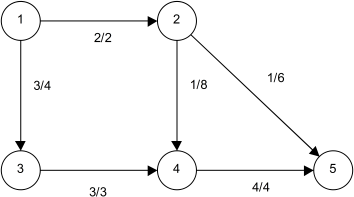
b) Dijkstra auf folgendem Graph ausführen:
c) Definiere (formal oder als Text) den Begriff "aufspannender Baum".
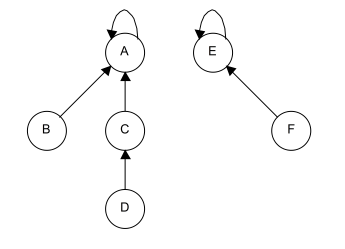
d) Führe union(D,F) auf folgender, als Wald realisierter disjunkter Menge aus:
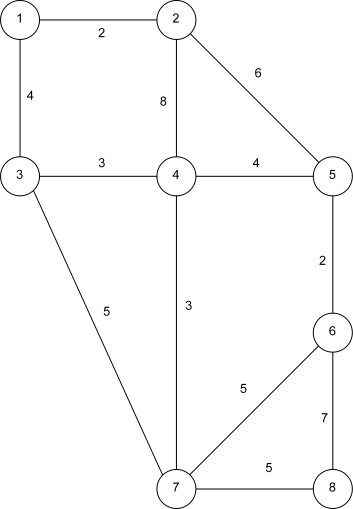
e) Erstelle den Restflussgraphen zu folgendem Flussgraphen:
Aufgabe 5: Übungsorganisation
Es herrscht grosser Andrang bei der Sprechstunde. Keiner der wartenden Studierenden erinnert sich an die genaue Ankunftsreihenfolge. Einige erinnern sich jedoch noch an die Leute die bereits warteten. Es soll eine ungefähre Ankunftsreihenfolge bestimmt werden.
| Name | wartete bereits |
|---|---|
| Annett | Daniel, Edeltraut |
| Bert | Anett, Daniel, Claudia |
| Claudia | - |
| Daniel | Claudia |
| Edeltraut | Claudia |
a) Erstelle einen Graph aus den Erinnerungen der wartenden Studierenden.
b) Nun soll die ungefähre Reihenfolge der Studierenden berechnet werden.
Algorithmus:
Ablauf:
Aufgabe 6: Dynamisches Programmieren
a) Geben Sie eine nicht-rekursive Java-Methode an, die g(m,n) für m, n e N \ {0} berechnet. Die Methode soll dafür polynomielle Laufzeit benötigen
b) Kleinste worst-case-Laufzeitklasse angeben:
O( .... )
Aufgabe 7: Geld wechseln
Gegeben ist ein Betrag, welcher durch möglichst wenige Geldstücke der Grössen { 200, 100, 50, 20, 10, 5, 2, 1 } dargestellt werden werden soll.
a) Geben Sie eine günstige Kodierung für die Geldstücke an
b) Geben Sie eine Zielfunktion und eine Optimierungsrichtung (max/min) an.
c) Geben Sie ein Greedy-Verfahren zur Lösung des Optimierungsproblems an (als Pseudocode oder verbal).